Tablas de Frecuencia Absoluta y Relativa
Las tablas de frecuencia son herramientas fundamentales en estadística para organizar y resumir datos. Permiten visualizar cómo se distribuyen los datos y facilitan su análisis.
Frecuencia Absoluta
La frecuencia absoluta ($f_i$) es el número de veces que aparece un valor específico en un conjunto de datos.
Ejemplo:
Consideremos las calificaciones de 20 estudiantes en un examen:
7, 8, 6, 9, 7, 8, 6, 7, 9, 10
6, 8, 7, 7, 6, 9, 8, 6, 7, 8
La tabla de frecuencia absoluta es:
| Calificación ($x_i$) | Frecuencia Absoluta ($f_i$) |
|---|---|
| 6 | 5 |
| 7 | 6 |
| 8 | 5 |
| 9 | 3 |
| 10 | 1 |
Frecuencia Relativa
La frecuencia relativa ($fr_i$) es el cociente entre la frecuencia absoluta y el total de datos ($N$):
$$ fr_i = \frac{f_i}{N} $$
Ejemplo Continuado:
Calculamos la frecuencia relativa:
| Calificación ($x_i$) | $f_i$ | $fr_i$ |
|---|---|---|
| 6 | 5 | $\frac{5}{20} = 0.25$ |
| 7 | 6 | $\frac{6}{20} = 0.30$ |
| 8 | 5 | $\frac{5}{20} = 0.25$ |
| 9 | 3 | $\frac{3}{20} = 0.15$ |
| 10 | 1 | $\frac{1}{20} = 0.05$ |
| Total | 20 | 1.00 |
Tipos de Gráficos para Representar Datos
Los gráficos son representaciones visuales que facilitan la interpretación de datos.
Gráfico de Barras
Muestra datos categóricos con barras cuya altura es proporcional a la frecuencia.
Ejemplo:
Gráfico de barras representando las frecuencias de calificaciones.
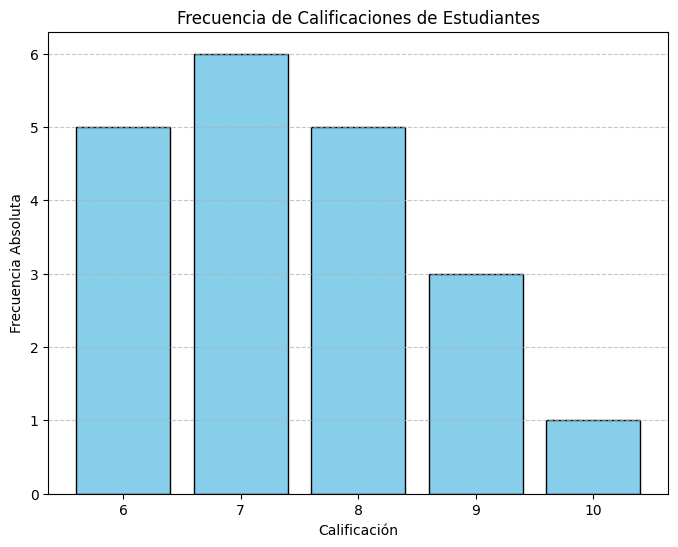
Gráfico de Pastel (Sectores)
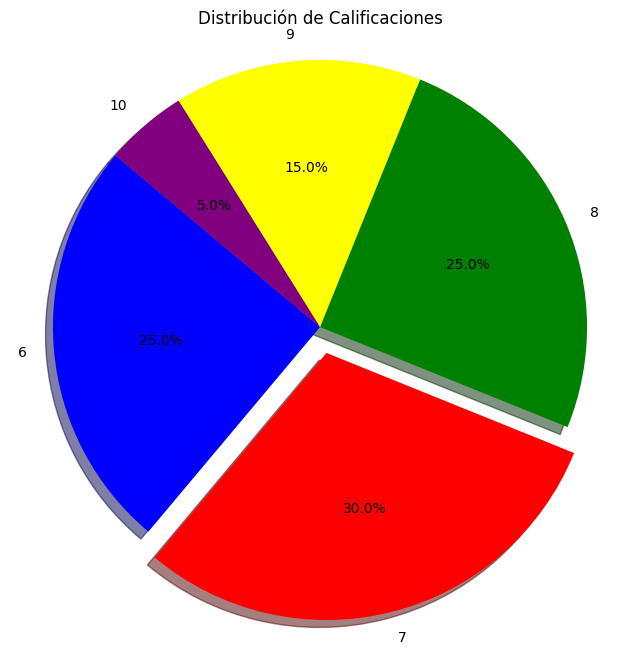
Representa proporciones de un todo mediante sectores circulares.
Ejemplo:
Gráfico de pastel representando las proporciones de calificaciones.
Histograma
Gráfico utilizado para datos continuos agrupados en intervalos.
Ejemplo:
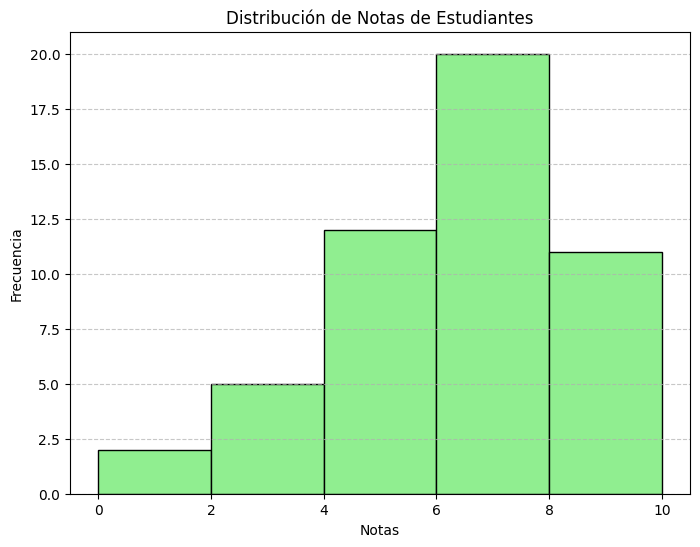
Notas de 50 estudiantes agrupadas en intervalos:
| Intervalo | Frecuencia |
|---|---|
| $[0,2)$ | 2 |
| $[2,4)$ | 5 |
| $[4,6)$ | 12 |
| $[6,8)$ | 20 |
| $[8,10]$ | 11 |
Histograma representando la distribución de notas de 50 estudiantes.
Polígono de Frecuencia
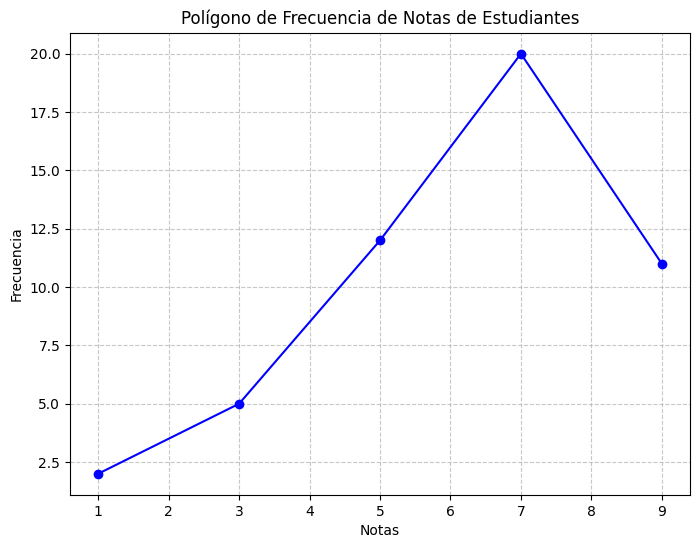
Gráfico que une los puntos medios de las cimas de un histograma.
Ejemplo:
Gráfico del polígono de frecuencia representando la distribución de notas.
Problemas que Involucran Tablas y Gráficos
Ejemplo 1: Encuesta de Preferencias
En una encuesta a 200 personas sobre su fruta favorita, se obtuvieron los siguientes resultados:
| Fruta | Frecuencia Absoluta |
|---|---|
| Manzana | 70 |
| Banana | 50 |
| Naranja | 40 |
| Pera | 30 |
| Uva | 10 |
Preguntas:
- ¿Cuál es la frecuencia relativa de cada fruta?
- Representar los datos en un gráfico de barras.
Solución:
- Calculamos la frecuencia relativa ($fr_i$):
| Fruta | $f_i$ | $fr_i$ |
|---|---|---|
| Manzana | 70 | $\frac{70}{200} = 0.35$ |
| Banana | 50 | $0.25$ |
| Naranja | 40 | $0.20$ |
| Pera | 30 | $0.15$ |
| Uva | 10 | $0.05$ |
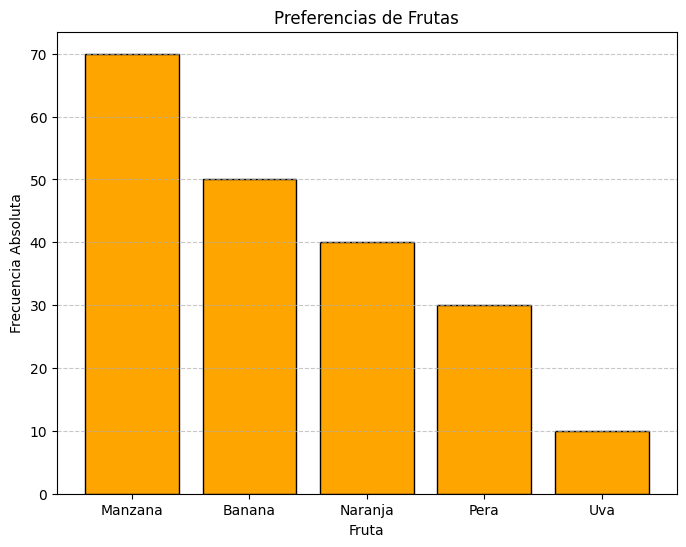
- Gráfico de barras:
Gráfico de barras representando las preferencias de frutas.
Ejemplo 2: Distribución de Edades
Una empresa tiene 100 empleados cuyas edades se distribuyen de la siguiente manera:
| Rango de Edad | Número de Empleados |
|---|---|
| 20-29 | 25 |
| 30-39 | 35 |
| 40-49 | 20 |
| 50-59 | 15 |
| 60-70 | 5 |
Pregunta: Construir un histograma que represente la distribución de edades.
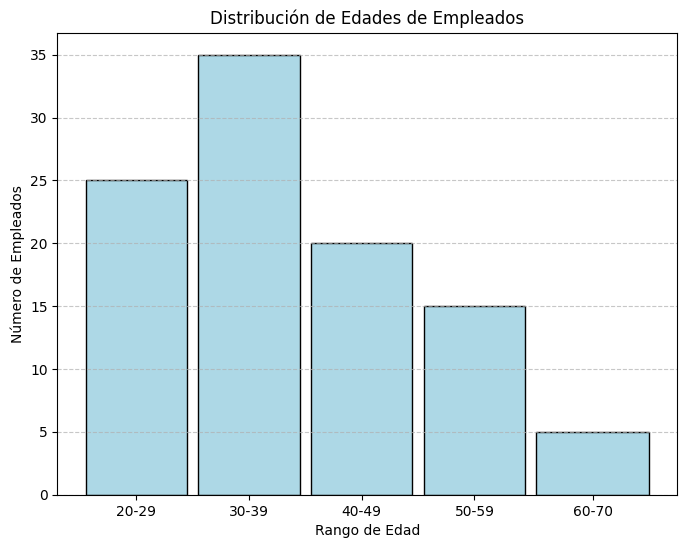
Solución:
Histograma representando la distribución de edades de los empleados.
Ejemplo 3: Ventas Mensuales
Una tienda registra las ventas mensuales de tres productos durante un trimestre:
| Producto | Mes 1 | Mes 2 | Mes 3 |
|---|---|---|---|
| A | 150 | 200 | 250 |
| B | 100 | 150 | 200 |
| C | 50 | 75 | 100 |
Pregunta: Representar la evolución de las ventas en un gráfico lineal.
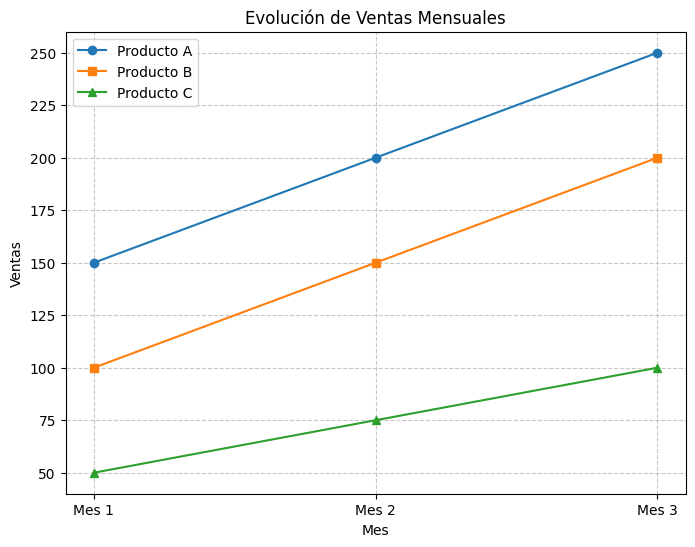
Solución:
Gráfico lineal representando la evolución de las ventas mensuales de los productos A, B y C.
Ejemplo 4: Temperaturas Diarias
Se registraron las temperaturas máximas durante una semana:
| Día | Temperatura ($^\circ$C) |
|---|---|
| Lunes | 25 |
| Martes | 27 |
| Miércoles | 26 |
| Jueves | 28 |
| Viernes | 30 |
| Sábado | 29 |
| Domingo | 27 |
Pregunta: Crear un gráfico que represente la variación de temperatura.
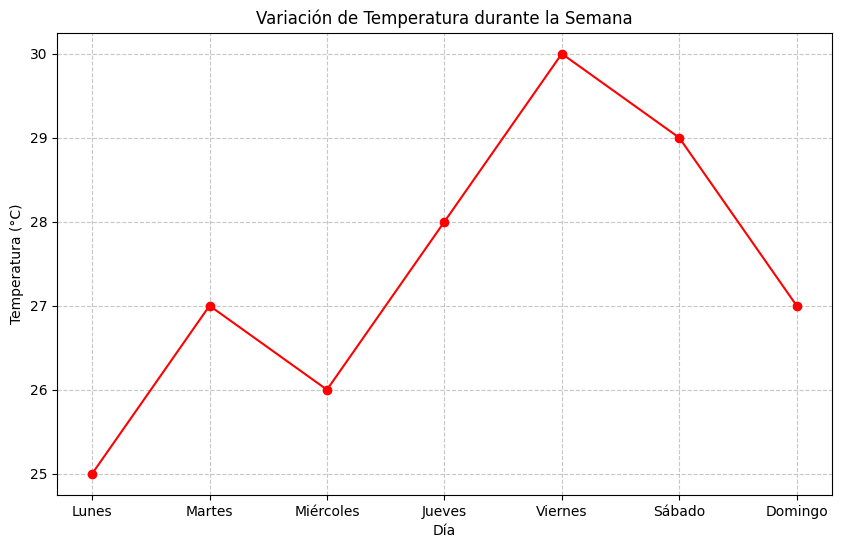
Solución:
Gráfico lineal representando la variación de temperatura durante la semana.
Conclusión
La representación de datos a través de tablas y gráficos es esencial para el análisis y comprensión de información estadística. Estas herramientas permiten identificar patrones, tendencias y relaciones que facilitan la toma de decisiones informadas.